Recursion

Recursion occurs when grammar production for a nonterminal references this nonterminal also on right-hand-side, either directly, or via other intermediate productions.

Context Free Grammar productions have fixed number of right-hand-side elements. To describe variable length sequence of elements recursion must be used.

If consecutive elements of sequence are to appear with no separators between them (should 'touch' each other) then recursive nonterminal must be placed either on very start or very end of recursive production. Such construction is called left- or right- recursion respectively.

This chapter describes parser operation with left and right recursion employed to process a sequence of elements. Language considered is a sequence of symbols a.

Left recursive grammar matching this language is:

Right recursive grammar for the same language is:

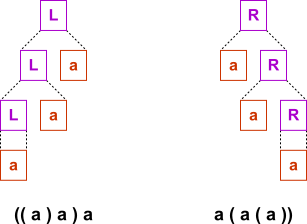
Example expansion of both these grammars is shown on Fig. 14.

Fig. 14 Left and right recursion

Left recursion

Automaton for left recursive grammar is:

Input sequence being parsed is a sequence of three symbols a:

Since grammar is left recursive, this input sequence will be parsed as:

To better illustrate parsing process each nonterminal stored on stack is indexed (L1, L2…) and is shown together with its source elements. Note that in reality such information is not present on stack.

Initial state:

Action for next input symbol a is to shift and go to state is #3:

In state #3 action is to reduce by production @2 if next input token is a:

In state #2 shift next input symbol a and go to state #4.

In state #4 action is to reduce by production @1:

Shift last a.

and reduce by production @1:

Since end of input was reached final state is accepting state. Parsing ends

Right recursion

Automaton for right recursive grammar is:

Input sequence being parsed is same as in previous example:

Grammar is right recursive, so input sequence will be parsed as:

Initial state:

First action is to shift a and go to state #3:

In state #3 action is to shift another a and return to the same state:

For third a action is the same

Since no more input remains next action is to reduce by production @2 to R:

In state #4 next action is again to reduce:

And once again:

Parser is accepting state. Parsing ends

Conclusions

LR(1) parsers work in bottom-up manner processing input from left to right.

When grammar is left recursive bottom-level productions appear first in input stream and can be completely reduced even before upper-level productions. As a result stack does not grow regardless of the depth of recursion.

When grammar is right recursive all productions are aligned with far end of input sequence. Until this end is reached, no production can be reduced. Input terminals being elements of these productions must be preserved which causes the stack to grow. Once end of input has been reached a chain of reductions occurs, collecting elements from stack, and wrapping them in nonterminals in bottom-up order. This continues until all elements on stack has been reduced to a single topmost nonterminal.

In either scenario reductions are fired in bottom-up order. In left-recursive variant reductions for low level productions are executed even before further input terminals has been read. In right-recursive scenario reductions are fired after all terminals has been successfully loaded.

Potential unlimited stack growth possible with right recursion should be avoided for performance and security reasons. In scenarios where either left or right recursion can be used, left should be preferred.