Context Free Grammar
Input to the parser is a sequence (stream) of terminal symbols (tokens) which should conform to a certain language. Definition of this language is given using Context Free Grammar (CFG). This type of grammar describes expected contents of input stream (or file) in a tree-like hierarchic way.
Compound constructs of grammar are expressed using nonterminal symbols. Each nonterminal is defined by means of productions. A production describes nonterminal's decomposition into lower-order elements which themselves can be both terminals and nonterminals. When several productions are defined for a single nonterminal, these provide alternative decompositions of this nonterminal.
Here is an example CFG grammar:
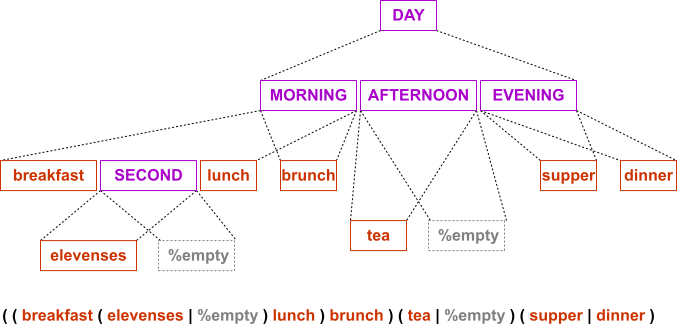
MORNING: breakfast SECOND lunch;
MORNING: brunch;
SECOND: elevenses;
SECOND: %empty;
AFTERNOON: tea;
AFTERNOON: %empty;
EVENING: supper;
EVENING: dinner;
CFG grammar is defined starting from topmost nonterminal (here DAY) down to level of terminal symbols. Alternative productions for nonterminals like MORNING result in multiple ways of expanding grammar down the tree. Possible grammar expansions are shown on Fig. 12.
Parsing CFG grammar requires working through input stream of nonterminals which corresponds to lowest level of grammar tree. During analysis upper levels of the tree are deduced from lower levels in a bottom-up fashion.
Term 'context-free' in CFG name means, that correctness of a nonterminal can be deduced from its lower-level elements without considering surrounding context. This means that if grammar contains rule as follows:
A combination of terminals a b found in input stream is sufficient to make a valid AB nonterminal.
It doesn't mean though that each sequence of a b constitutes an AB. Consider grammar:
@2 ABX: A BZ;
@3 AB: a b;
@4 C: c;
@5 A: a;
@6 BZ: b z;
And input of form:
First two input terminals a b might potentially constitute a nonterminal AB. However such assumption would make it impossible to parse rest of input since next terminal is z and no expansion of grammar matches sequence AB z. Only after analyzing entire input it becomes clear that in this case decomposition should be:
A -> a
BZ -> b z
Above example illustrates one fact: parsing CFG grammar in general requires analyzing entire input from start to end, and considering all alterative interpretations of this input, until a matching one is found.

Alpag uses LR(1) parsing algorithm which reads input linearly from left to right. It does not wait until end of input stream to globally resolve all ambiguities. Instead it attempts to recognize grammar phrases on-the-fly. This means that parser cannot process grammars which require reading input to the very end before making decision on interpretation of earlier symbols. As a consequence it cannot handle all CFG grammars, but only a subset of them.
It is possible that user defines a valid CFG grammar, but Alpag is not able to build parser for it and reports an error. Grammar can be sometimes reworked to match LR(1) algorithm limitations, however in general building a parser for such grammar with Alpag may be not possible.